平衡状態とは
こうして水の一部が電離するわけですが、電離して生じたH+とOH-が水中で衝突すると、再び水に戻るという反応が起こります。つまり
H2O⇔H++OH-
という反応式が表しているのは
H2O→H++OH-
H++OH-→H2O
という二つの反応が同時に起こっているということです。水が電離すれば、H+とOH-が増えます。増えると、逆反応(水に戻る反応)も起こりやすくなります。1.0×10^-7〔mol/l〕という濃度は、この兼ね合いで決定するのです。
しかし、電離して濃度が1.0×10^-7〔mol/l〕になると反応が止まる、ということではないんです。
後に述べるように反応が同じ速さで起きているために見かけ上反応が止まったように見えるんです。 この状態を平衡状態といいます。
反応速度
ここからの話は、厳密には化学Ⅱの反応速度論・化学平衡が絡んでくるのですが、出来るだけ簡単に解説したいと思いますので、分かりにくい箇所は質問箱の方へ是非よろしくお願いします。
さて、ここで1Lの水を考えます。
H2O=18、水の密度は1g/cm3ですから、水1Lというのは物質量に換算すると
1000 ――――=55.5≒56mol 18となります。
ところで、電離する水の濃度は1.0×10^-7〔mol/l〕でしたよね。つまり8桁違うんです。8桁下のほうで上がったり下がったりされてもまったく影響はないと見て構いませんよね。誤差に紛れてしまうんです。ですから次のように言うことが出来ます。
水の物質量について、電離の影響は無視できるほど小さいので、電離しても水の物質量は変わらないと近似できる。
しかし電離して生じたH+は「小さいから」という理由で無視することは出来ません。無視というのは「無視しても話に影響しない」「無視しても計算結果に影響しない」から無視するんです。
H+を無視するということは「電離そのものを無視する」ということです。いまは電離を無視すると話が出来ませんから無視は出来ません。
ところで、Aという物質とBという物質からABという物質が出来る反応
A+B→AB
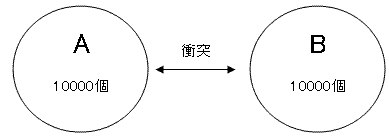
について、左辺の濃度を変えたときに、どのように反応が変わるかについて考えます。仮にAとBが共に1L中に10000個あったとします。これらは水中に散らばっていますが、たまにAとBが衝突します。衝突しても必ず反応が起きるとは限りませんが、ある確率で反応しABになります。
そのABに戻る確率を考えます。
しかし「“衝突したときに”水に戻る確率」は一定ですから、濃度を変えることによって衝突する確率を考えます。
コレを基準に考えます

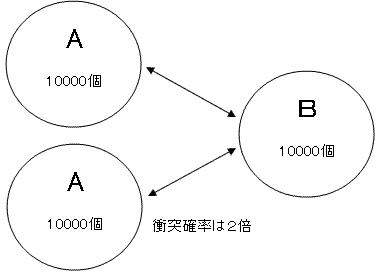
ここでAだけ20000個になったとします。つまり2倍になったのですが、このとき衝突する確率も2倍になります。Bだけが2倍になったとしても同じですね。
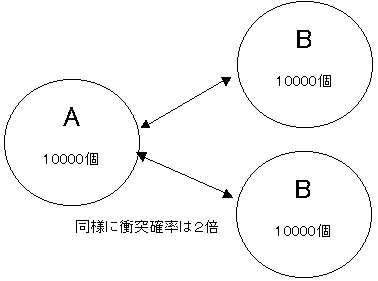
もし片方だけが3倍になったとしたら、衝突確率は3倍です。
しかしどちらも2倍になったとしたらどうでしょうか。衝突する確率ですから、これは2×2=4倍になりますね。
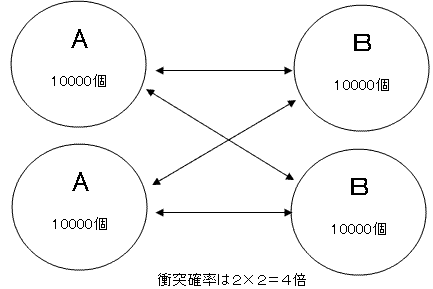
さらに、Aが2倍、Bが3倍になったとしたらどうでしょうか。これも2×3=6倍になります。
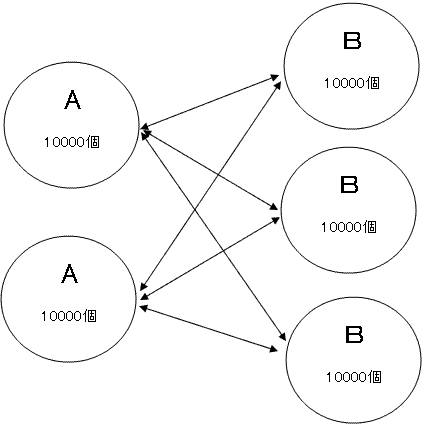
これらのことから「衝突確率は濃度の積に比例する」ということがわかります。
したがって、1秒間に1Lあたりに反応した物質の物質量を反応速度というのですが、このことについて次のように言うことが出来ます。
反応速度
反応速度は、反応物の濃度の積に比例し、反応速度vは、比例定数をkとして次のように書ける。
v=k[A][B]
[A]、[B]はそれぞれAの濃度、Bの濃度を表しますね。つまり(Aの濃度)×(Bの濃度)ということです。
水のイオン積
水の電離について、この式を適用してみましょう。
正反応(水の電離)の反応物はH2Oですから、反応速度v1は水の濃度に比例しますね。
v1=k1[H2O]・・・式1
H2Oの濃度といわれてもピンと来ないかもしれませんが、水1Lに相当する物質量とみて構いません。次いで逆反応(水に戻る反応)の反応速度v2は、H+とOH-の濃度の積に比例しますね。
v2=k2[H+][OH-]・・・式2
では電離に関する平衡状態について考えていきます。
平衡状態とは正反応と逆反応が同じ速さで行われているために、見かけ上反応が停止した状態を指します。
反応が進むと、反応物や生成物の濃度が変わりますね。するとあるとき、v1とv2が等しくなるような濃度の条件が実現します。これが平衡状態です。
水の電離について考えると、式1、式2についてv1=v2となるような濃度が平衡状態です。したがって次の等式が成立します。
k1[H2O]=k2[H+][OH-] k1 [H+][OH-] ―=――――――― k2 [H2O]
ここでk1とk2はともに定数ですから、まとめることができます。このまとめた定数をKとおくと、次の式が成立します。
[H+][OH-] K=―――――――・・・式3 [H2O]
ここでKは平衡定数といい、温度によって決まる定数です。
つまり温度が同じであれば、最初の濃度条件にかかわらず、平衡時の右辺の値は一定ということが出来ます。逆に言えば、初期条件に関係なく、平衡時には右辺の値がKとなるように[H+][OH-][H2O]の値が動きます。
ところで[H2O]は、前述のとおり、電離によって変化しないものと見て良いわけです。ということは[H2O]は変わらないから定数ですね。式3について定数を左辺に移すと
K[H2O]=[H+][OH-]
そして定数どうしはまとめて新たな定数とすることが出来ます。K[H2O]=Kwとおくと次の式が成立します。
Kw=[H+][OH-]・・・式4
このKwを水のイオン積といいます。(添え字wはwaterの頭文字です)
水のイオン積は、前述のとおり温度が同じなら常に同じ値です。この値を求めてみましょう。
25℃において[H+]=[OH-]=1.0×10-7〔mol/l〕というのは計測済みですから、25℃における水のイオン積は
Kw=[H+][OH-]=1.0×10-7×1.0×10-7=1.0×10-14〔mol2/l2〕
これは酸や塩基の影響で水溶液の[H+]や[OH-]が変わっても成立します。このことと、イオン積の値は、非常に重要です。必ず覚えてください。
