原子の酸化状態
酸化還元反応とは、何度も書いているように、原子同士で電子を受け渡しする反応のことです。第一章の一番最初に説明した銅の酸化についてもう一回見てみましょう。
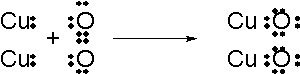
この現象を電子の授受という立場から説明してみます。ここで生成した酸化銅というのはイオン結合の物質であり、銅が電子を放出して酸素がそれを受け取っているんでしたね。これはまさに電子の移動、酸化還元反応です。
このとき銅がどれだけの電子を酸素に渡し、酸素がどれだけの電子を奪ったのかを考えることにします。これを原子の酸化状態といいます。原子の酸化状態を考えることが、次の章の半反応式につながってきます。
銅の酸化の場合で考えてみましょう。はじめは酸素も銅も単体ですから、電子を取ったり取られたりしてはいません。すなわちニュートラルな状態にあります。ですが反応すると電子のやりとりが起きますね。その結果としてできたのが酸化銅です。酸化銅になったとき、酸素原子はO2-になりました。これはニュートラルな状態と比べて酸素が電子を二つ奪ってきた状態ですね。この状態のことを酸素の酸化数は-Ⅱであるといいます。
次に銅原子はCu2+に変化しましたが、これはニュートラルな状態と比べて電子を二つ奪われた状態だといえます。この状態のことを銅の酸化数は+Ⅱであるといいます。
ここで出てきた酸化数という用語は、ニュートラルな状態(単体のとき)と比べて、自分の保有する電子がどのくらい増減しているかを表しています。
酸化数と酸化還元反応
重要なのは、酸化還元反応をすると、電子のやり取りをした分だけ酸化数が変化するということです。そういう風に人間が決めたのです。これは便利な概念ですよ。
具体的には、酸化されると酸化数が増加し、還元されると酸化数が減少します。増減の数は、やりとりした電子の数と同じです。この知識は、ある種の頻出問題を解くのには役に立ちます。
酸化数の具体例
もっと具体的な物質の酸化数を考えてみましょう。 今回は、硝酸と一酸化窒素について考えてみることにします。
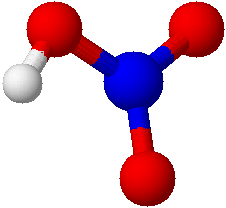
硝酸HNO3
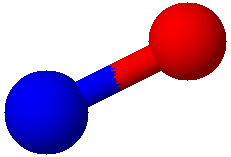
一酸化窒素NO
青が窒素 赤が酸素 白が水素原子を表す。
二つとも窒素酸化物ですが、窒素の酸化状態はどちらも異なります。それぞれ窒素がどのような酸化数になっているか考えてみましょう。
硝酸のルイス構造式は次のように書けます。
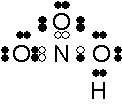
注※白球はNの価電子
硝酸に含まれるNの酸化状態を考えてみましょう。まず電気陰性度においてN<Oです。また、Nがもともと持っている価電子の数は5です。(窒素は15族でしたね)構造式を見るとその価電子がすべて共有結合に使われているのがわかります。なので、5個とも酸素に奪われたと考えられます。この状態は酸化数+Ⅴですね。
次に一酸化窒素に含まれるNの酸化状態を考えます。一酸化窒素のルイス構造式は次のように書けます。
注※白球はNの価電子
構造式を見ると、価電子のうち2つが共有結合に使われているのが分かります。なのでこの2つが酸素に奪われて、酸化数は+Ⅱということができます。
このように、同じ元素の化合物でも酸化の度合いが違うということが分かると思います。ある酸化数から違う酸化数へ動く時に電子の授受が行われて酸化還元反応が起こるのです。
酸化数の簡単な求め方
ですが、酸化数を求めるのにいちいちルイス構造式を書いていては面倒です。なので簡単な酸化数の求め方があります。ここではそれを紹介しましょう。
簡単に言うと、酸素がくっつくと2つ電子を奪うし、水素がくっついたら1つ電子をくれるという設定で解けばいいんです。
- 単体の酸化数は0である
- 単原子イオンの酸化数は、イオンの価数に一致する
- 化合物の場合、各原子の酸化数の和は0である
- 多原子イオンの場合、各原子の酸化数の和はイオンの価数に一致する。
- 水素の酸化数は+Ⅰである
- 酸素の酸化数は-Ⅱである
ルールが多くて大変ですが、慣れると簡単です。さっきの二つの例で考えてみましょう。
硝酸の場合、Hが1つでOが3つあり、化合物なので酸化数の和は0です。なのでNの酸化数をxとすると
1+(-2)×3+x=0 ∴x=+5
一酸化窒素の場合、Oが1つなので同様にして
-2+x=0 ∴x=+2
となります。結果は一致しますね。
これは練習問題を何個か解いて身につけるしかないと思います。酸化還元の基礎演習(クリックすると酸化数の問題に飛びます)という練習のページを作ったので、気が向いたらやっていってください。
